Velocidad instantánea

Se define la velocidad instantánea o simplemente velocidad como el límite de la velocidad media cuando el intervalo de tiempo considerado tiende a 0. También se define como la derivada del vector de posición respecto al tiempo. Su expresión viene dada por:

v→=limΔt→0v→m=limΔt→0Δr→Δ t=dr→dt

donde:

• v→ : Vector velocidad instantánea. Su unidad de medida en el Sistema Internacional es el metro por segundo ( m/s )
• v→m : Vector velocidad media. Su unidad de medida en el Sistema Internacional es el metro por segundo ( m/s )
• Δr− : Vector desplazamiento. Su unidad de medida en el Sistema Internacional es el metro ( m )
• Δ t : Intervalo de tiempo que tiende a 0, es decir, un intervalo infinitamente pequeño. Su unidad de medida en el Sistema Internacional es el segundo ( s )

La velocidad es una magnitud vectorial. Su ecuación de dimensiones viene dada por [v]= LT-1

¿Cómo se deduce la expresión de la velocidad instantánea?

Para definir el concepto de velocidad instantánea con precisión vamos a partir del concepto de velocidad media que hemos estudiado con anterioridad y vamos a ayudarnos de la gráfica de la figura.

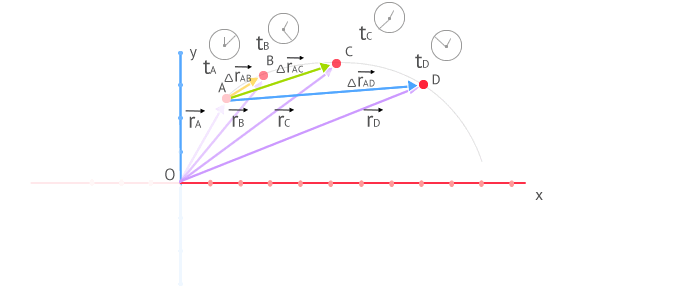
El procedimiento para definir la velocidad instantánea o, simplemente, velocidad en un punto A consiste en calcular la velocidad media entre A y un punto lo más próximo posible a A. Esto se traduce en calcular la velocidad media en un intervalo de tiempo lo más pequeño posible. En la gráfica puedes ver el vector de posición del punto A y del resto de puntos B, C y D. Estos son r→A , r→B  , r→C  y r→D  respectivamente. Además está representado el vector desplazamiento entre A y cada uno de los puntos B, C y D. Estos son Δr→AB , Δr→AC y Δr→AD respectivamente. Como puedes ver en la gráfica anterior, a medida que el segundo punto es más próximo a A, el vector desplazamiento, se va haciendo tangente a la trayectoria y su módulo se aproxima al valor del espacio recorrido sobre la trayectoria.

EJEMPLO:

Si un cuerpo se mueve según la siguiente ecuación:

r(t)−→− = (4⋅t + t2)⋅i→+4⋅t⋅j→ m

Calcula su velocidad instantánea en el instante t=1sg.

Datos

r(t)−→− = (4⋅t + t2)⋅i→+4⋅t⋅j→ m

Resolución

Para resolver este problema haremos uso de la siguiente ecuación, que establece que la velocidad instantánea es la derivada con respecto al tiempo del vector de posición. 

v→=limΔt→0v→m=limΔt→0Δr→Δ t=dr→dt

Derivando o realizando el límite, obtenemos que:

v(t)−→− = (4+ 2⋅t)⋅i→+4⋅j→ m

Una vez que conocemos el vector de la velocidad instantánea, sustituimos el valor de t=1sg y obtendremos la velocidad instantánea para dicho instante:

v(1)−→− = (4+ 2⋅1)⋅i→+4⋅j→ m ⇒v(1)−→− = 6⋅i→+4⋅j→ m